ABSTRACT:
This thesis presents high performance forward error correcting codes suitable for random and burst errors. It initially verifies the performance of burst error correcting convolutional codes.
Then constructed codes are combined with other high performance random error correcting codes to form new schemes of serially concatenated codes. The performance of newly proposed codes is tested under random and burst error channels and compared with other well-known codes to investigate their effectiveness in constructing a reliable error protection system for different applications.
SNIPPETS:
Digital Communication Systems:
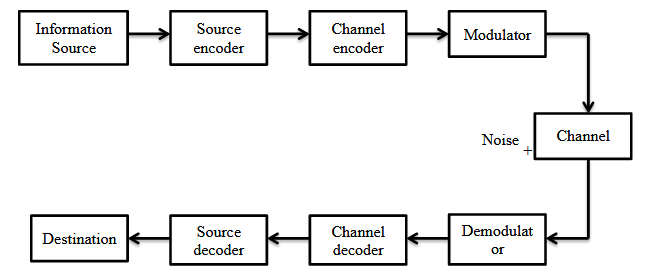
Figure 1.1 shows the fundamental components of a digital communication system. Source and destination are physically separated points. When the signal travels in the communication channels, noise interferes with it.
The addition of noise in the original signal disturbs the message content. Therefore the received message by the receiver may not match the original message. Thus,the transmission rate of the signal is restricted by the presence of noise and disturbances in the communication channel.
Types of Errors:
There are two main types of error in transmission systems. They are random and burst errors. Random errors are inconsistent and do not affect the performance of the system in following intervals. These errors are uncorrelated and developed due to the noise in the memory less channels. They are found in a transmission channel that requires line-of-sight transmission.
Error Control Technique:
In digital communication systems when reliable and efficient data transfer is considered error control technique plays an important role. By using various coding schemes the channel errors are reduced to an acceptable level to ensure the quality of data transmission.
For this reason, different types of algorithms have been designed to detect and correct the errors. All these algorithms have common features of adding extra redundancy to the original information during the transmission, which in turns are removed by the decoder at the receiver.
Types of Codes:
Different FEC coding methods are used in the digital communication systems. They are mainly classified into block and convolutional codes.
CONVOLUTIONAL CODES
Convolutional Coding:
Convolutional coding is another important FEC coding technique. This method of coding is more used in communication channel with a memory. The implementation of convolutional codes is found in applications, which requires good performance and low computational complexity.
Unlike block codes, convolutional codes operate on code streams. It convertsany length of message to a single codeword. The name convolutional coding is given because the output bit stream of the encoder is convolution of input data it and the transfer function of the encoder.
State Diagram of Convolutional Codes:
State diagram is another important method to analyse and represent convolutional codes. It is a graphical view of all the possible sates of the encoder and the possible moved form one to another state.
It shows the relationship between the state, input and output of the encoder. The state diagram has 2(K-1)k nodes, where each node represents one encoder state. The nodes of the state diagram connect the branches. Every node has 2k entry branches entering it and 2k outgoing branches.
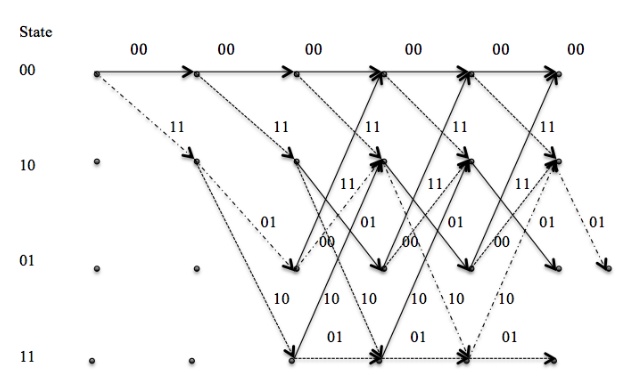
Trellis Diagram:
A trellis diagram is an extended representation of state diagram. For each instant of time it shows all the possible states. A unique path through the trellis represents the input bits and output bits.
Trellis Truncation and Termination:
Trellis truncation is the simple method in which the encoder is reset to zero at the beg inning of bit shifting operation. After each bit is shifted, no extra bits are shifted to put the encoder into initial state. The typical example of trellis truncation is the trellis diagram shown in Figure 2.7.

Figure 2.7 Shows the Trellis Truncation for Message u=(1,0,1,1,0,0) Applied in(2,1,2) Convolutional Code.
Interleaved Convolutional Codes:
Burst-error is mostly found in storage and wireless communication systems. The presence of burst-error is corrected by interleaving technique. Interleaved convolutional codes for correcting burst-error was first introduced by Hagelbarger. The general idea behind using interleaving is to spread the long burst of error into random error. For some communication systems, long burst-error is not correctable.
DECODING CONVOLUTIONAL CODES
Decoding of Convolutional Codes using Viterbi Algorithm:
Viterbi algorithm wasfirst proposed by Andrew Viterbi as a decoding algorithm for convolutional codes in 1967. It is also known as a maximum likelihood decoding process, which uses trellis structure to find the codeword closest to the received message. Viterbi algorithm searches all the likely paths in the trellis and compares the metrics between each path. The metrics here used is branch metrics and pah metrics.
Hard decision decoding of convolutional codes using Viterbi algorithm:
In hard decision decoding of convolutional codes, the message received from the noisy channel are quantized into the two levels of binary data either ‘0’ or ‘1’. These binary data are fed into the decoder as an input. The next step follows the procedure of finding most likelihood path along the trellis structure. It involves the calculation of finding the minimum Hamming distance between the surviving paths.
Soft decision decoding of convolutional codes using Viterbi algorithm:
Unlike hard decision decoding, in soft decision decoding, bits received by the decoder from the channelare quantized into more than two levels. Long length of the soft decision level will increase performance in expense of increasing the computational difficulty. Decoding is carried out according to the quantization level. The number of zeros and ones in the quantization level determines the strongest and weakest bit.
Decoding Burst Error Using an Interleaved System:
A simple feedback decoding circuit for correcting single error is given below . This single error correcting decoder circuit can be converted into burst error correcting decoder by an interleaving technique. The interleaving degree (lamda )introduced during the convolutional encoding has to be used again after the codeword is received.
CYCLIC CODES
Cyclic Codes:
Cyclic codes are considered as a very special case of linear block codes. A linear block code C of (n, k) system is considered a cyclic if cyclically shifted code vector of block code C generates a code vector of the same code C. For example let c= c0, c1, c2, c3 …cn-1 is a codeword oflinear (n, k)block codeandits cyclic shift denoted by c’= n-1,c0, c1, c2, c3…cn-2is also a codeword if it belongs to the codeword in the (n, k)block code C.
Generator Polynomial:
A cyclic code is based on a generator polynomial denoted by g(X) . The number of codewords that can be derived from an(n, k) code is 2k. Every valid codewords of (n, k) code will have a polynomial of degree at least n-kbut they cannot have degree more than n-1.
Properties of Cyclic Codes:
Generally the generation of cyclic codes can be defined by its properties.
The nonzero code polynomial of minimum degree in a cyclic code C is unique. 2.In an (n, k) cyclic code, there exists one and only code polynomial of degree n-k which is given by g(X) = g0+ g1X + g2X2 + g3X3 +…+ gn-2-1Xn-2+ Xn-k. where g0 and gn-k-1arealways 1.3.The generator polynomial g(X) of an (n, k)cyclic code is a factor of Xn+ 1.4.The generator polynomial g(x) generates an (n, k)cyclic code, if g(X) is a polynomial of degree n-kand is a factor of Xn+ 1.
Calculation of Syndrome and Error Detection:
After the encoding of message, depending upon the systematic and non systematic form of G matrix the codeword is obtained. Suppose c= c0, c1, c2,…, cn-1 as codeword considered for transmission through the channel.
DECODING CYCLIC CODES
Decoding and Correction of Burst Error Using Cyclic Codes:
The codes that are only designed for random error correction are not sufficient and do not provide an efficient and the reliable transmission system. The occurrence of burst error in digital media and communication is certain. For example in radio signal transmissionof mobile communications, the interference over short time intervals can cause bursts errors. Thereare some codes to correct burst errors.
Zero Spans and Zero Span Coverings of Parity Check Matrices:
The zero spans of parity check matrices is defined as a sequence of successive zeros between two nonzero components in a vector over GF(q). A vector in a circulant parity check matrices may contain more than one zero spans.
Burst Decoding of (n, k) Cyclic Codes:
Suppose a code word c = c0, c1,…, cn-1 of an (n, k)cyclic code is transmitted through a channel and the vector received is r = r0, r1,…, rn-1. Assume that the received vector has an error. This is expressed by r = c + e and e= e0, e1, …, en-1 is the burst error of length b≤B(Hn0).
SIMULATION RESULTS
Simulations are done by using MATLAB software. They are carried out to analyse the results of the research and make important conclusion. Simulation includes the following procedures:
- Millions of random bits as message are generated.
- Random bits are divided into number of blocks.
- Blocks of message a re passed through the proposed encoder.
- Codewords generated from the proposed encoders are passed through the different models of channel such as BSC and AWGN channels.
- The received codewords are then passed through the proposed decoder.
- The decoded blocks of message are then compared with the original blocks of message.
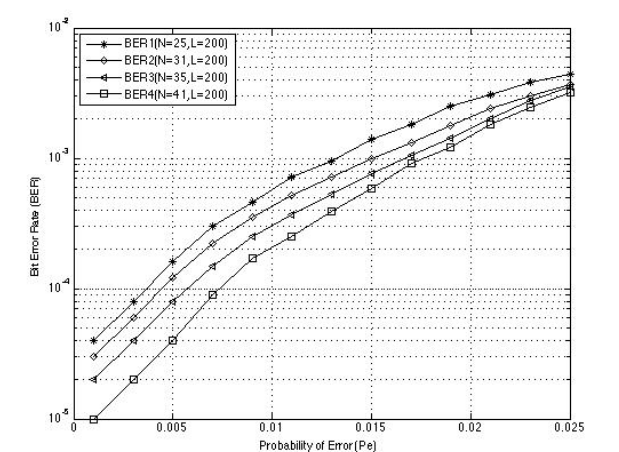
- After that the Bit Error Rate(BER)is calculated.
Simulation of Interleaved Convolutional Codes:
SUMMARY AND CONCLUSION
In this thesis, burst error correcting convolutional codes, cyclic codes and both random and burst error correcting concatenated codes, which are very important for the broadband wireless transmission systems were discussed. The introduction and basic terminology used in error correction were given in Chapter 1.
In Chapter 2, the structure and encoding of convolutional codes were studied. Similarly the design of interleaved convolutional codes that are used for the detection and correction of burst errors were discussed.
The decoding of convolutional codes based on Viterbi algorithm were presented in Chapter 3. The details in decoding with trellis structure of Viterbi algorithm was also studied. Similarly, the decoding of interleaved convolutional codes to correct the burst errors was discussed.
In Chapter 4, the encoding structure and parity check matrix of (n, k) cyclic codes were studied. Whereas, in Chapter 5,the burst decoding of cyclic codes based on circulant parity check matrix were discussed.
Due to the advancement in digital communication systems, forward error correction coding techniques have been implemented for years to allow efficient and excellent data communications over noisy channels.
It can be concluded that the main reasons of using error correcting codes is gaining the ability to provide reliable transmission over different kinds of channels. The coding technique should be based on the type of errors expected (for example,burst errors and random bit errors) .
Coding techniques with higher error detection and correction capability will use more redundant bits and bandwidth. This reduces information transmission rates and will increase the delay for encoding and decoding at source and destination. Thus, on the design of higher error correcting codes the factor affecting the transmission rate should be wisely considered.
Source: Charles Darwin University
Author: Sundar Rupakheti
>> More Matlab Projects on Signals and Systems for Engineering Students
>> 200+ Matlab Projects based on Control System for Engineering Students
>> More Matlab Projects based on Wireless Communication for Engineering Students
>> More Wireless Communication Projects in Matlab for Engineering Students