ABSTRACT
Over the past decade, several security issues with Linux Random Number Generator (LRNG) on PCs and Androids have emerged. The main problem involves the process of entropy harvesting, particularly at boot time. An entropy source in the input pool of LRNG is not transferred into the non-blocking output pool if the entropy counter of the input pool is less than 192 bits out of 4098 bits. Because the entropy estimation of LRNG is highly conservative, the process may require more than one minute for starting the transfer. Furthermore, the design principle of the estimation algorithm is not only heuristic but also unclear. Recently, Google released an Internet of Things (IoT) operating system called Brillo based on the Linux kernel.
We analyze the behavior of the random number generator in Brillo, which inherits that of LRNG. In the results, we identify two features that enable recovery of random numbers. With these features, we demonstrate that random numbers of 700 bytes at boot time can be recovered with the success probability of 90% by using time complexity for 5.20 × 240 trials. Therefore, the entropy of random numbers of 700 bytes is merely about 43 bits. Since the initial random numbers are supposed to be used for sensitive security parameters, such as stack canary and key derivation, our observation can be applied to practical attacks against cryptosystem.
STRUCTURE OF LRNG AND BRILLO
There are two ways to generate random numbers from these entropy pools (blocking pool and non-blocking pool). /dev/random is used to produce random numbers from the blocking pool, and /dev/urandom or get_random_bytes() is used to generate random numbers from the non-blocking pool. The difference between the two methods lies in the usage of the entropy counter.
In the case of the blocking pool, the entropy is transferred up to the requested size until the entropy counter is sufficiently large to generate secure random numbers. On the other hand, random numbers are immediately generated from the non-blocking pool regardless of its entropy counter. Figure 1 depicts the procedure and building blocks of LRNG.
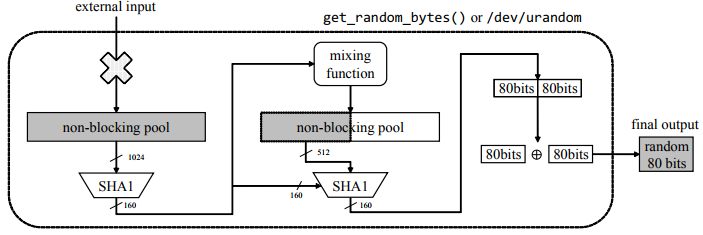
Figure 2. Extract unit:Extracting random numbers using get_random_bytes() or / dev / urandom without the entropy transfer
Most of the random numbers are produced through the get_random_bytes() function. This function internally uses Secure Hash Algorithm 1 (SHA-1) and LFSR-based mixing function. First, output of the 160 bits is generated from the non-blocking pool through SHA-1. Then, it is again injected through the mixing function into the non-blocking pool.
Next, 512 bits of the non-blocking pool and previously generated output of 160 bits are entered into SHA-1. Then, output of 160 bits is generated. This output is split into the most significant 80 bits and the least significant 80 bits, which are then eXclusive-OR (XOR)-ed. Finally, get_random_bytes() generates 80 bits of random numbers. This extraction process is referred to as an extract unit when the cost of recovery is calculated (Figure 2).
ANALYZING FEATURES OF LRNG DURING BOOT PROCESS
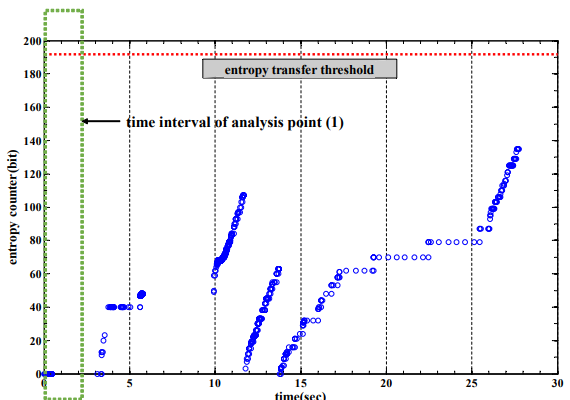
Figure 5. Entropy counter of the input pool during boot time in Brillo
Figure 5 indicates a typical graph for the entropy counter. The entropy counter is less than 192 bits during boot time. Therefore, generating random numbers by /dev/urandom or get_random_bytes() is “almost” deterministic because there is no entropy transfer from the input pool to the non-blocking pool.
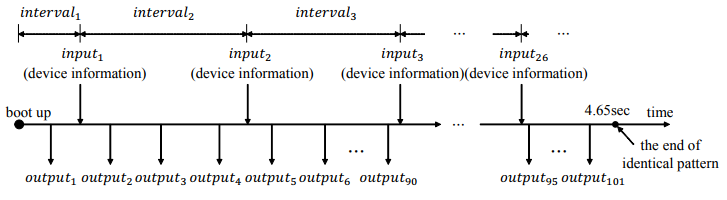
Figure 8. Timeline for identical pattern at boot time in Brillo
The first feature (insufficient entropy) is unique to LRNG. This feature is also satisfied in Brillo and makes LRNG generate random numbers without any entropy transfer. The second feature (identical pattern) is a unique one that is observed during boot time of Brillo. By combining the two features, recovering random numbers between intervel1 and intervel3 depends on cycles. therefore, cycles is the most important factor to recover random numbers in these intervals.
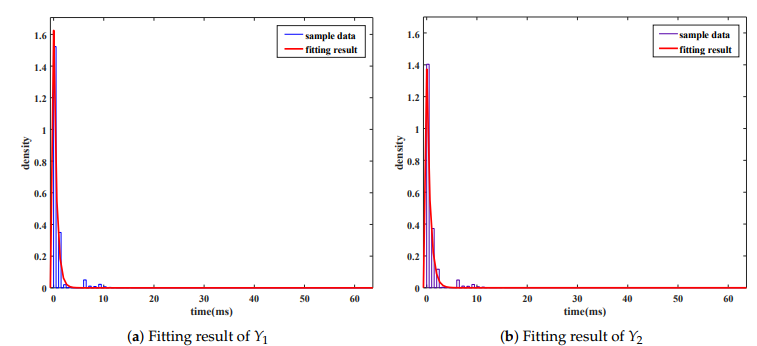
Figure 10. Fitting results for sample values of Y1 and Y2 . (a) Fitting result of Y1 ; (b) Fitting result of Y2
By using distribution fitting tool of MATLAB, we confirm several properties of the distributions. Fitting results show that the sample values converge on the exponential distributions (Figure 10).
EXPERIMENTAL RESULTS FOR SUCCESS PROBABILITIES AND COSTS
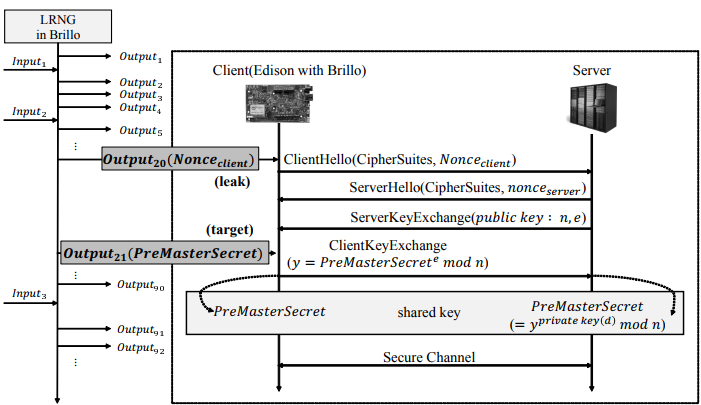
Figure 11. Scenario to recover random numbers during boot time
For example, if output20 used in a nonce value of Client Hello of SSL, output21 becomes the PreMasterSecret. It is encrypted with the public key of the server and then transmitted from the client to the server. After this communication, both the client and server generate the shared master key. Because output20 is exposed in the public channel, an attacker can obtain ouput20 and compromise the state of the non-blocking pool by using the leak value as a discriminant.
Figure 11 depicts this scenario. According to this scenario, we implemented a program to recover random numbers of 700 bytes between interval1 and interval3 using ouput20 with α = 2.09 and β = 2.49. As the results, it requires 12 h to find the right value with approximate 235 trials of the extract unit (SHA-1 × 2 + mixing function × 1). It is not a real-time analysis on a single PC. However, the attack program can be drastically accelerated with parallel computing.
SEVERAL COUNTERMEASURES
We determined that two features of LRNG exist in Brillo. Using these features, the random numbers of 700 bytes during boot time of Brillo can be recovered with the probability of 90% time complexity for 5.02 × 240 trials of extract unit. Two approaches for mitigating this vulnerability can be considered. One can be immediately applied, and the other requires systematic works.
- Simple methods to apply
- Methods requiring systematic research
CONCLUSIONS
LRNG has several security problems while operating on a PC and smartphone. We investigated whether identical problems occur in the Linux-kernel-based operating system, Brillo. We observed two features of LRNG when operating during Brillo boot time. Random numbers of 700 bytes can be recovered with the probability of 0.90 by the cost of 5.20 × 240. In conclusion, the entropy of random numbers of 700 bytes is approximately 43 bits. This means that structural improvements and theoretical analysis of its security are required. Various methods can be proposed to improve security.
In the future, we will study LRNG in three perspectives. The first will be to analyze unknown usage of remaining random numbers. The results can be used to find several vulnerabilities for the init process and cryptographic libraries. Secondly, we are planning to consider brand-new boards and their hardware properties later because these boards may expose different features with Edison. Lastly, we will study efficient use of entropy sources in terms of the design. In order to overcome LRNG inefficiency and conservatism, several efficient methods are needed to enable optimal usage of the noise sources.
Source: Kookmin University
Authors: Taeill Yoo | Ju-Sung Kang | Yongjin Yeom
>> Top IoT Projects using Matlab for B.E/B.Tech Students
>> 200+ IoT Led Projects for Engineering Students
