ABSTRACT
The mobile satcom antenna (MSA) enables a moving vehicle to communicate with a geostationary Earth orbit satellite. To realize continuous communication, the MSA should be aligned with the satellite in both sight and polarization all the time. Because of coupling effects, unknown disturbances, sensor noises and unmodeled dynamics existing in the system, the control system should have a strong adaptability.
The significant features of terminal sliding mode control method are robustness and finite time convergence, but the robustness is related to the large switching control gain which is determined by uncertain issues and can lead to chattering phenomena. Neural networks can reduce the chattering and approximate nonlinear issues. In this work, a novel B-spline curve-based B-spline neural network (BSNN) is developed.
The improved BSNN has the capability of shape changing and self-adaption. In addition, the output of the proposed BSNN is applied to approximate the nonlinear function in the system. The results of simulations and experiments are also compared with those of PID method, non-singularity fast terminal sliding mode (NFTSM) control and radial basis function (RBF) neural network-based NFTSM. It is shown that the proposed method has the best performance, with reliable control precision
MODELING OF A MOBILE SATCOM ANTENNA
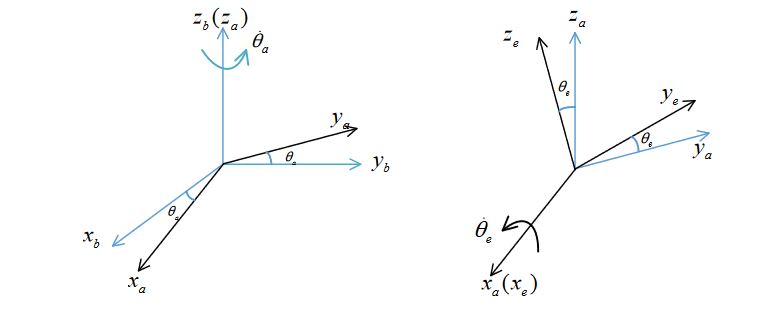
Figure 1. Coordinate definition and transformation
The paper focuses on a double gimbal MSA. The innermost gimbal is an elevation gimbal on which the antenna array is mounted, while the outmost gimbal is an azimuth gimbal which is mounted on the base. According to the coordinates system definition and the conversion relationships between different coordinates, a dynamic model of the mobile satcom antenna is derived.
B-SPLINE NEURAL NETWORK
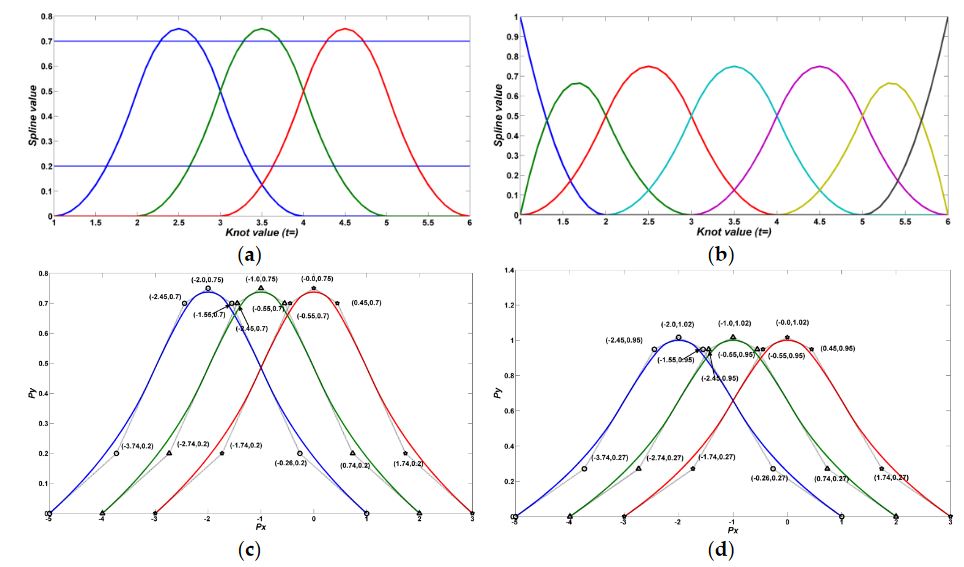
Figure 3. (a) Order 3 B-spline basis function in which the internal knot vector
If the first knot and the last knot have multiplicity with value k + 1, the B-spline curve is called closed clamped; otherwise, it is called an open clamped B-spline curve. More specific illustrations can be seen in Figure 3.
RESULTS OF EXPERIMENT AND SIMULATION

Figure 5. Experimental two axis MSA system
Experiments and simulations were carried out to validate the performance of the proposed BSNN-based NFTSM control method in this section. The experimental system is shown in Figure 5. Comparisons are made between the results of the conventional PID method, the TSM in reference, the NTSM in reference, the NFTSM in this paper, the RBF neural network-based NFTSM.
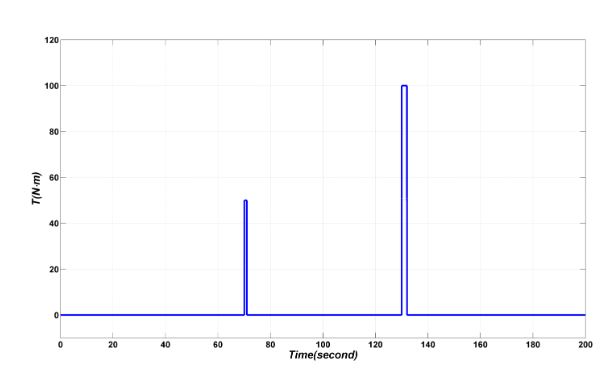
Figure 12. Pulse disturbances added to the system
In order to validate the disturbance rejecting ability of the proposed method, pulse disturbances of 50 N·m and 100 N·m are added at time 70 s and 130 s, respectively, as shown in Figure 12.
CONCLUSIONS
The paper focuses on the inertial sensor-based two gimbal mobile satcom antenna. In order to obtain high quality communications, the MSA should point to the specific satellite when the carrier is moving. The dynamic model of MSA is established based on traditional Newton-Euler method and the corresponding control block diagram is built. In this paper, the non-singular fast terminal sliding mode control is adopted and developed to increase the line of sight stabilization accuracy. Meanwhile, the features of existence and convergence in finite time are proved.
Then a neural network is employed to approximate the nonlinear item in the system. In addition, a novel BSNN is proposed and used in this paper. A brief study of B-spline basis and B-spline function is also carried out, then the computational function used to obtain the arbitrary point on the curve is derived. The B-spline function is reformed to enhance its adaptive capacity. To validate the effectiveness of the proposed NFTSM and BSNN, simulations and experiments are conducted.
Results of different methods, including PID, NFTSM, NFTSM-RBF, NFTSM-BSNN, are compared in this paper. It is shown that the proposed method has better decoupling effects and disturbance rejecting ability than the others. Because the B-spline curve has an excellent ability called “local control”, it can be used to approximate arbitrarily shaped curves. According to the analysis in this paper, we can conclude that the proposed BSNN is good at nonlinear approximation owing to its local features. The robustness of the system can also be improved by applying this method.
Source: Beihang University
Authors: Xiaolei Zhang | Yan Zhao | Kai Guo | Gaoliang Li | Nianmao Deng
>> 60+ Antenna Communication Projects for Engineering Students